
 
excerto

Barras de Cuisenaire
Os Materiais Manipulativos Como Mediadores no Processo de Ensino e
Aprendizagem em Matemática
Os conceitos matemáticos podem ser difíceis para os alunos entenderem em
virtude de sua natureza abstrata. Nesse sentido, é importante que os professores
tenham como foco facilitar o entendimento desses conceitos ao invés de preparar
os alunos para praticar e decorar os procedimentos de rotina (NCTM, 2000).
A utilização de materiais manipulativos nas salas de aula de matemática apoia
essa abordagem, pois possibilita que os alunos compreendam os conteúdos
matemáticos, permitindo-os descobrirem e aplicarem os conceitos propostos em
sala de aula (CLEMENTS e BATTISTA, 1990).
Os materiais manipulativos são objetos concretos que podem ser fisicamente
manipulados pelos alunos para demonstrar ou modelar conceitos matemáticos
abstratos. Esses materiais incluem, por exemplo, o Tangram, os Cubos, o Material
Dourado e as Barras de Cuisenaire.
Quando devidamente empregados, esses materiais tornam a aprendizagem de
conteúdos curriculares agradáveis para os alunos. Entre o final da década de
1960 e início da década de 1970, houve uma ampliação da presença de materiais
manipulativos em salas de aula, principalmente da educação infantil, com a
justificativa teórica elaborada por Zoltan Dienes (1916-2014) sobre como as
estruturas matemáticas podem ser ensinadas com a utilização desses materiais.
A partir desse trabalho, no processo de ensino e aprendizagem de conteúdos
matemáticos, foram utilizados os materiais manipulativos na prática pedagógica,
possibilitando aos alunos a aquisição do senso numérico, aritmético, geométrico
e algébrico (DICKSON, BROWN e GIBSON, 1984).
A utilização contínua dos materiais manipulativos tem um efeito positivo no
desempenho dos alunos, pois permitem a utilização de objetos concretos para
observar, modelar e internalizar os conceitos matemáticos (MILLER e O’NEIL,
2004). Esses materiais auxiliam os alunos a construírem os seus modelos
matemáticos, além de serem vantajosos para motivar os alunos na aprendizagem de
conteúdos matemáticos (SMITH, 2002).
De acordo com Piaget (1965), as crianças começam entender os símbolos e os
conceitos abstratos após as experiências realizadas no nível concreto. Por isso,
os materiais manipulativos são ferramentas eficientes para auxiliar os alunos na
construção de conhecimentos abstratos.
Dessa maneira, a aprendizagem de alunos com deficiência, como por exemplo, os
cegos, podem ser beneficiados pela utilização de materiais manipulativos
(FERNANDES, 2011). Por se tratar de alunos cegos, o papel dos professores é
muito importante para auxiliar esses alunos na compreensão de conceitos
propostos no currículo escolar. Então, é importante ressaltar que a:
(...) falta de acuidade visual é uma deficiência do tipo sensorial, cuja
principal característica é a carência ou comprometimento de um dos canais de
aquisição da informação – o visual. A fim de minimizar os efeitos dessa
carência, que podem comprometer o desenvolvimento cognitivo dos deficientes
visuais, as situações de aprendizagem para esses indivíduos devem ser mediadas
de forma distinta das situações apresentadas aos aprendizes com acuidade visual
dentro dos padrões normais (HEALY e FERNANDES, 2009, p. 1).
De acordo com essa citação, essa abordagem pode ser eficaz para promover a
interação dos alunos com deficiência visual com o conhecimento matemático. Com
relação aos alunos com deficiências visuais, existe a necessidade de que os
materiais manipulativos sejam adaptados às suas necessidades para possibilitar a
“efetiva inclusão dos alunos cegos na escola” (PEIXOTO, PIMENTA e SILVA, 2011,
p. 38).
Assim, a adaptação desses materiais possibilita que os alunos cegos possam
perceber o relevo com o tato por meio da utilização de diferentes texturas e
contrastes, como, por exemplo, o liso ou o áspero e o fino ou o espesso. Essa
abordagem pedagógica possibilita que os alunos cegos reconheçam e discriminem as
partes que compõem o todo de um determinado objeto, pois esses alunos podem
desenvolver e exercitar as habilidades requeridas para a realização das tarefas
(SÁ, 2011) propostas em sala de aula.
Nesse contexto, é importante que se proponha a utilização das barras adaptadas
do material manipulativo de Cuisenaire para ensinar as operações de adição e
subtração para alunos cegos, sendo necessária, então, a adaptação desse material
com o objetivo de viabilizar esse aprendizado.
Teoria da Mediação
Vygotsky iniciou os seus estudos na área de educação especial em 1924 quando
trabalhou no Instituto de Psicologia Experimental de Moscou, na Rússia. Seus
trabalhos eram otimistas, pois destacavam que as deficiências, como, por
exemplo, a cegueira e a surdez somente significavam a lacuna de um dos caminhos
para o acesso ao ambiente, que poderia ser substituído por outro (HEALY e
FERNANDES, 2011).
Os estudos do desenvolvimento das crianças com deficiências foram denominados de
Defectologia, cujo conceito está relacionado com as investigações das
dificuldades de aprendizagem de alunos da educação especial, que têm
deficiências sensoriais (auditivas, fala ou visão), deficiências motoras, bem
como deficiências no funcionamento cognitivo (SMAGORINSKY, 2012).
Assim, a educação defectológica foi desenvolvida destacando a importância que a
educação tem ao atender as necessidades especiais dos alunos com deficiências
por meio da elaboração de um sistema especial de signos culturais e símbolos que
devem ser adaptados às suas características específicas (VYGOTSKY, 1993).
De acordo com essa perspectiva, há uma ênfase na mediação por meio da utilização
desse sistema simbólico fundamental para mediar as ações entre os alunos com
suas deficiências e os conteúdos (VYGOTSKY, 1993) curriculares, visando
potencializar as habilidades desses alunos. Então, a noção de mediação, que é:
(...) central em Vygotsky, funda-se não só na fala oral, mas em situações
interativas, nas quais instrumentos, gestos, signos e outros elementos que fazem
parte do meio transformam processos interpessoais em intrapessoais (HEALY e
FERNANDES, 2011, p. 230).
Dessa maneira, a formulação de conceitos matemáticos está relacionada com o
processo de aprendizado que necessita do auxilio de um conjunto de fatores
externos e signos, que mediam as imagens que são formadas pelos alunos durante o
processo de apropriação do conhecimento. Esse conjunto de signos é considerado
como um mediador interno que funciona como uma ferramenta auxiliar que é
utilizada para transformar os objetos (REGO, 1995) que estão disponibilizados no
ambiente.
Nesse contexto, a mediação ocorre por meio da interação entre os sujeitos e o
mundo de maneira intermediada por ferramentas pedagógicas que estão relacionadas
com a linguagem e com os materiais concretos e manipuláveis (MOYSÉS, 2012).
Assim, a relação dos seres humanos e, consequentemente, dos alunos com
deficiências, com o mundo “não é direta, mas é uma relação mediada e complexa
que se realiza por meio de dois tipos de mediadores: os instrumentos e os
signos” (VYGOTSKY, 1987 apud MANRIQUE e FERREIRA, 2010, p. 15).
Inicialmente, os indivíduos produzem os signos, que podem ser considerados como
representações de suas experiências cotidianas. Assim, à medida que essas
representações são compartilhadas, ou seja, representadas por meio dos mesmos
signos, as experiências semelhantes para diferentes indivíduos podem
possibilitar a emergência de uma nova série de processos cognitivos, que
ultrapassam a existência individual de cada indivíduo e estabelecem um novo
plano desses processos psíquicos, que é o social (MOYSÉS, 2012).
No entanto, para que esse compartilhamento possa ocorrer, é necessário que se
crie um sistema de signos que seja expresso por meio de sua materialização no
mundo. Dessa maneira, a linguagem é entendida em sua ampla gama de
manifestações, pois pode ser considerada como um sistema de signos por
excelência. Por exemplo, a linguagem pode ser expressa por meio da língua
falada, que é um sistema de símbolos que identificam regras de comportamento a
serem realizados, como, por exemplo, as placas de trânsito ou os sinais que
identificam as quantidades e as suas relações como os números e os sinais de
operações matemáticas.(MOYSÉS, 2011)
Dessa maneira, o conceito de mediação é empregado quando são empregados
elementos intermediários na relação de ensino e aprendizagem (VYGOTSKY, 1998).
Nesse sentido, a relação dos alunos com o ambiente de aprendizagem não é direta,
mas mediada pelo material de Cuisenaire adaptado, que funcionou como mediador no
processo de ensino e aprendizagem das operações de adição, subtração e
multiplicação.
Material Manipulativo de Cuisenaire
O material manipulativo de Cuisenaire ou as Barras de Cuisenaire são versáteis e
utilizados para ensinar conteúdos matemáticos diversificados, como, por exemplo,
as quatro operações básicas, as frações, as áreas e os volumes de figuras
geométricas, as raízes quadradas, as equações lineares e quadráticas e os
sistemas de equações. Essas barras foram denominadas de Cuisenaire por causa de
seu inventor Georges Cuisenaire (1891-1976), que foi um professor belga, que
inventou essas réguas coloridas de madeira para ensinar aritmética para os seus
alunos.
Figura 1: Barras de Cuisenaire

Fonte: Arquivo pessoal da professora-pesquisadora
Entretanto, a popularização dessas barras para o ensino de matemática foi
desenvolvida por Caleb Gattegno (1911-1988), um educador e matemático egípcio,
que conduziu pesquisas e investigações em matemática, em educação matemática, em
linguística e em psicologia, que foram conduzidas, principalmente, pelas
preocupações sociais relacionadas com o continente africano.
Em suas propostas educacionais, Gattegno proporcionava a possibilidade de
matematização de situações associadas aos problemas concretos encontrados no
cotidiano e, por meio da dedução e da indução, os alunos poderiam associar os
conceitos matemáticos a essas situações.
(Nesse contexto, a matematização é o processo por meio do qual os indivíduos
utilizam ferramentas matemáticas distintas para auxiliá-los na organização,
análise, compreensão, entendimento, modelação e resolução de problemas
específicos enfrentados no cotidiano. Essas ferramentas possibilitam a
descoberta de relações e regularidades, a esquematização, a formulação e a
visualização de situações-problema de maneiras diferenciadas, traduzindo-as do
mundo real para a conceituação matemática cotidiana (ROSA e OREY, 2006).) Em 1953, Gattegno conheceu o trabalho
de Georges Cuisenaire. Impressionado com o potencial pedagógico e matemático
desse material, Gattegno iniciou a utilização dessas barras para ensinar
conteúdos matemáticos diversificados para os seus alunos (POWELL, 2004).
Nesse direcionamento, o potencial pedagógico das Barras de Cuisenaire também
pode ser utilizado para o processo de ensino e aprendizagem de crianças cegas
com a devida adaptação desse material manipulativo por meio da substituição das
cores das barras por texturas. Iniciou-se, então, durante o meu estudo, um
processo didático-pedagógico para a substituição das cores das barras por texturas, contudo,
mantendo as características básicas das Barras de Cuisenaire por meio das quais
existe uma associação entre as cores e os números.
Figura 2: Associação entre as cores o números nas Barras de Cuisenaire
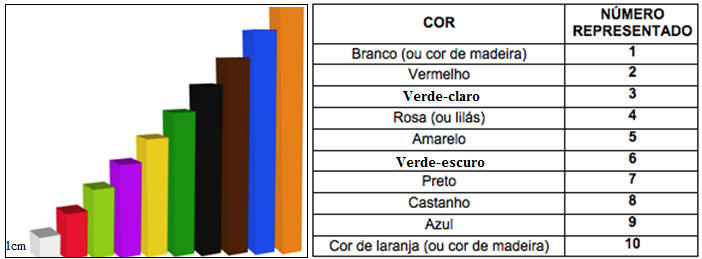
Fonte: Arquivo pessoal da professora-pesquisadora
O conjunto de barras de Cuisenaire é um material de base 10, que é composto por
barras com dez tamanhos diferentes, em formato de prismas quadrangulares e
confeccionados em madeira e com cores padronizadas. Os comprimentos variam de 1
a 10 centímetros, sendo utilizadas para auxiliar no desenvolvimento da
coordenação motora; da memória, da comparação, percepção de forma, tamanho e
cores (COELHO, COSTA, TAVARES e ALVES 2010).
Material Manipulativo de Cuisenaire Adaptado
O ensino de matemática proporciona o desenvolvimento das habilidades do
pensamento lógico e do raciocínio dedutivo, pois auxilia os alunos a aprenderem,
procurarem e descobrirem as ideias por si mesmos por meio da descrição, da
categorização, da direção, da quantidade, das formas e dos atributos lógicos.
Assim, a descrição de conceitos matemáticos que necessitam da visualização pode
ser adquirida com facilidade pelos alunos videntes, porém, os alunos com
deficiências visuais e os cegos requerem o desenvolvimento de um processo
cognitivo mais amplo para a aquisição desses conceitos (DICK e KUBIAK, 1997).
O currículo matemático para os alunos cegos deve conter o mesmo conteúdo a ser
trabalhado com os alunos videntes, não devendo omitir quaisquer conteúdos
julgados mais difíceis ou abstratos, pois esta omissão pode causar discrepâncias
na aprendizagem desses conteúdos por esses alunos (NAPIER, 1973).
Por exemplo, os resultados do estudo conduzido por Stevens (1996) mostram que o
desempenho de alunos com deficiências visuais em matemática têm sido baixo por
causa da dificuldade que possuem em aprenderem os conceitos matemáticos. Nesse
sentido, as metodologias de ensino utilizadas para o entendimento dos conceitos
matemáticos devem ser adaptadas às necessidades específicas desses alunos.
Nesse contexto, a “aprendizagem de qualquer conceito matemático fica facilitada
quando comparada com objetos concretos” (BRANDÃO, 2004 apud SILVA, 2010, p. 31)
por meio da utilização de materiais manipulativos.
Figura 3: Aluno manipulando o Material de Cuisenaire Adaptado

Fonte: Arquivo pessoal da professora-pesquisadora
Com o intuito de modificar o quadro da situação do ensino de matemática para
alunos cegos, é importante focalizar também no ensino das operações de adição e
subtração com o auxílio das barras adaptadas do material manipulativo Barras de
Cuisenaire.
Então, para substituir as cores, sem, contudo perder o propósito do trabalho com
as Barras de Cuisenaire, optou-se pela substituição de cores de mesma família,
por barras de mesma textura, mesmo que representando tamanhos diferentes.
Dessa maneira, as barras de tamanhos 2, 4 e 8, que no material original de
Cuisenaire seriam representadas por cores de mesma família, no material adaptado
das barras de Cuisenaire foram substituídas por barras de mesma texturas e
colocadas em potes de mesma cor.
Figura 4: Material de Cuisenaire e o Material de Cuisenaire Adaptado

Fonte: Arquivo pessoal da professora-pesquisadora
No material original, o número 1 é aquele que cabe em todos os outros, logo é
utilizada a cor branca ou da madeira para representá-lo. O número 7 é
representado pela cor preta, é primo e não corresponde com outro número de 1 até
10, a não ser o 1 e o próprio 7. Nessa adaptação, optou-se a textura lisa para
representar esses números.
No material de Cuisenaire original esses números são representados pelas cores
branca e preta, respectivamente. Contudo, a opção para representar essas barras
com texturas iguais ocorreu com o objetivo de evitar confusão no caso de se
introduzir uma nova textura para esses números.
Como os números 2, 4 e 8 representam as potências de 2: 2¹, 2² e 2³ foram
utilizadas como textura duas ranhuras paralelas nas bases das barras. Dessa
maneira, como os números 3, 6 e 9 são múltiplos de 3, foram utilizadas ranhuras
perpendiculares às bases das barras. Para a representação dos números 5 e 10,
que são múltiplos, foi utilizada uma textura de lixa na extremidade das barras.
Outro detalhe importante utilizado nessa adaptação foi o tamanho das barras,
pois as barras originais são pequenas para que sejam manipulação por alunos
cegos. Nesse sentido, as peças de tamanho 1 podem se perder sobre a mesa devido
ao seu tamanho diminuto. Dessa maneira, a barra que representa o tamanho 1 foi
adaptada com as medidas de 2cm x 2cm x 2cm e, na sequência, as demais barras
tiveram suas alturas aumentadas em 2 cm em relação à altura da barra
correspondente no material adaptado.
[...]
Esse livro traz várias atividades matemáticas desenvolvidas com o auxílio das
Barras de Cuisenaire. Contudo, como essas atividades não são contextualizadas, o
tratamento com as barras é realizado de uma maneira diferente do usual, pois a
contextualização ocorre por meio da manipulação das próprias barras por meio da
relação entre as suas características, como, por exemplo, tamanho, numeração e
texturas. Dessa maneira, com o auxílio da professora de apoio, é possível
contextualizar as atividades para abordar os conteúdos matemáticos propostos em
sala de aula.
A Ludicidade como um Recurso Pedagógico para o Processo de Ensino e Aprendizagem
em Matemática
É importante ressaltar a importância do aprender brincando, pois os alunos
demonstram na realização das atividades propostas em sala de aula, a satisfação
em manipular as barras adaptadas. Nesse contexto, a aprendizagem deve ser
concebida por meio do lúdico e da manipulação, do concreto para o abstrato,
sendo, portanto, necessário enfatizar que o:
(...) brinquedo cria na criança uma nova forma de desejos a um “eu” fictício, ao
seu papel no jogo e suas regras. Dessa maneira, as maiores aquisições de uma
criança são conseguidas no brinquedo, aquisições que no futuro tornar-se-ão seu
nível básico de ação real e moralidade (VYGOTSKY, 1998, p. 131).
De acordo com essa asserção, constata-se que existe uma influência que os
brinquedos ou os materiais manipulativos têm no desenvolvimento dos alunos.
Então, essa abordagem proporciona uma possibilidade pedagógica de trabalho para
os professores em sala de aula por meio da mediação didática. Nesse, sentido, a:
(...) esfera cognitiva é particularmente ativada com a utilização de brinquedos,
pois sua manipulação é inerentemente motivadora de ações em situações
imaginárias, o que permite à criança aprender “a dirigir seu comportamento não
somente pela percepção imediata dos objetos ou pela situação que a afeta de
imediato, mas também pelo significado dessa situação (VYGOTSKY, 1998, 127).
Então, os alunos fazem o que mais gosta de fazer, porque os brinquedos ou os
materiais manipulativos estão unidos ao prazer e, ao mesmo tempo, aprendem a
seguir os caminhos mais difíceis, subordinando ao que querem, uma vez que a
sujeição à regra e a renúncia à ação impulsiva constitui o caminho para o prazer
nesses materiais (VYGOTSKY, 1984).
Nesse contexto, os materiais manipulativos destacam-se por apresentar um caráter
de materiais educativos concretos que servem de suporte para o ensino de
conteúdos matemáticos, sendo, portanto, muito interessantes na utilização
cotidiana da sala de aula.
Então, os alunos podem desenvolver a ludicidade quando utilizam as barras
adaptadas do material manipulativo de Cuisinaire para aprender os conceitos
matemáticos de adição, subtração e multiplicação, bem como para brincar por meio
da construção de muros, casas e escadas, ao mesmo tempo em que resolvem os
problemas propostos em sala de aula.
Assim, devido à variedade da utilização das barras adaptadas do material
manipulativo de Cuisenaire, essa apropriação lúdica relacionada com as
atividades bi e tri dimensional desse material podem possibilitar uma conexão
dos alunos com os problemas de adição e subtração, bem como com aqueles nos
quais os conceitos de multiplicação que podem emergir durante a realização das
atividades que foram propostas de uma maneira concreta (COELHO, COSTA, TAVARES e
ALVES, 2010).
Nesse sentido, a percepção dos conceitos matemáticos (adição, subtração,
multiplicação, crescente/decrescente, entre outros) podem adquirir sentido para
os alunos, pois ao realizarem as atividades propostas de uma maneira livre,
apropriando-se do material adaptado e observando a sua utilização para além da
realização das atividades matemáticas, como, por exemplo, de maneira lúdica para
tornar o ato de aprender prazeroso e divertido.
Similarmente, a apropriação lúdica do material manipulativo também auxilia no
desenvolvimento da atividade perceptiva dos alunos, pois o:
(...) crescimento da criança vai evidenciar que, por meio do brinquedo, ela
liberta seu pensamento para que não fique estritamente ligado aos estímulos
perceptuais. Ela consegue imaginar uma situação, desligando-se do mundo
material, concreto do qual tem contato, desenvolvendo assim capacidade de se
desprender do real significado do objeto, (da madeira, por exemplo), podendo
imaginá-lo como um boneco (ROLIM, GUERRA e TASSIGNI, 2008, p. 180).
De acordo com Vygotsky (1998), essa apropriação lúdica que está expressa na
atividade de brincar com o material manipulativo pode possibilitar que os alunos
participem de uma experimentação cognitiva por meio da qual essas barras
adaptadas não sejam utilizadas de uma maneira meramente manipulativa, pois
auxilia-os na articulação e na simbolização dos problemas matemáticos de adição,
subtração, direcionando-os para o desenvolvimento do raciocínio multiplicativo.
Dessa maneira, ressalta-se a importância da ludicidade no processo de ensino e
aprendizagem dos conceitos matemáticos pelos alunos.
FIM
ϟ
excerto de
As Barras Adaptadas de Cuisenaire como Mediadoras do Processo de Ensino e Aprendizagem das Operações de Adição, Subtração e Multiplicação para Alunos Cegos do Ensino Fundamental I
autora: Marianna Drummond
Produto Educacional
Mestrado Profissional em Educação Matemática
ICEB - UFOP
2016
|



